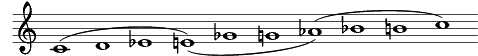Mode of limited transposition

Modes of limited transposition are musical modes or scales that fulfill specific criteria relating to their symmetry and the repetition of their interval groups. These scales may be transposed to all twelve notes of the chromatic scale, but at least two of these transpositions must result in the same pitch classes, thus their transpositions are "limited". They were compiled by the French composer Olivier Messiaen, and published in his book La technique de mon langage musical ("The Technique of my Musical Language").

Technical criteria

Based on our present chromatic system, a tempered system of 12 sounds, these modes are formed of several symmetrical groups, the last note of each group always being common with the first of the following group. At the end of a certain number of chromatic transpositions which varies with each mode, they are no longer transposable, giving exactly the same notes as the first.

There are two complementary ways to view the modes: considering their possible transpositions, and considering the different modes contained within them.

Definition by chromatic transposition

Transposing the diatonic major scale up in semitones results in a different set of notes being used each time. For example, C major consists of C, D, E, F, G, A, B, and the scale a semitone higher (D♭ major) consists of D♭, E♭, F, G♭, A♭, B♭, C. By transposing D♭ major up another semitone, another new set of notes (D major) is produced, and so on, giving 12 different diatonic scales in total. When transposing a mode of limited transposition this is not the case. For example, the mode of limited transposition that Messiaen labelled "Mode 1", which is the whole tone scale, contains the notes C, D, E, F♯, G♯, A♯; transposing this mode up a semitone produces C♯, D♯, F, G, A, B. Transposing this up another semitone produces D, E, F♯, G♯, A♯, C, which is the same set of notes as the original scale. Since transposing the mode up a whole tone produces the same set of notes, mode 1 has only 2 transpositions.

Any scale having 12 different transpositions is not a mode of limited transposition.

Definition by shifting modal degrees

Consider the intervals of the major scale: tone, tone, semitone, tone, tone, tone, semitone. Starting the scale on a different degree will always create a new mode with individual interval layouts—for example starting on the second degree of a major scale gives the "Dorian mode"—tone, semitone, tone, tone, tone, semitone, tone. This is not so of the modes of limited transposition, which can be modally shifted only a limited number of times. For example, mode 1, the whole tone scale, contains the intervals tone, tone, tone, tone, tone, tone. Starting on any degree of the mode gives the same sequence of intervals, and therefore the whole tone scale has only 1 mode. Messiaen's mode 2, or the diminished scale, consists of semitone, tone, semitone, tone, semitone, tone, semitone, tone, which can only be arranged 2 ways, starting with either a tone or a semitone. Therefore, mode 2 has two modes.

Any scale having the same number of modes as notes is not a mode of limited transposition.

Messiaen's list

Messiaen's first mode, also called the whole-tone scale, is divided into six groups of two notes each. The intervals it contains are tone, tone, tone, tone, tone, tone – it has two transpositions and one mode.

The second mode, also called the octatonic, diminished, whole-half, or half-whole scale, is divided into four groups of three notes each. It contains the intervals semitone, tone, semitone, tone, semitone, tone, semitone, tone – it has three transpositions, like the diminished 7th chord, and two modes:

The third mode is divided into three groups of four notes each. It contains the intervals tone, semitone, semitone, tone, semitone, semitone, tone, semitone, semitone – it has four transpositions, like the augmented triad, and three modes.

The fourth mode contains the intervals semitone, semitone, minor third, semitone, semitone, semitone, minor third, semitone – it has six transpositions, like the tritone, and four modes.

The fifth mode contains the intervals semitone, major third, semitone, semitone, major third, semitone – it has six transpositions, like the tritone, and three modes.

The sixth mode has the intervals tone, tone, semitone, semitone, tone, tone, semitone, semitone – it has six transpositions, like the tritone, and four modes.

The seventh mode contains the intervals semitone, semitone, semitone, tone, semitone, semitone, semitone, semitone, tone, semitone – it has six transpositions, like the tritone, and five modes.

Expansion and alteration of the modes

Are there others?

Messiaen wrote, "Their series is closed, it is mathematically impossible to find others, at least in our tempered system of 12 semitones." More modes can be found that fit the criteria, but they are truncations of the original seven modes. Indeed, all these modes can be regrouped mathematically speaking in a lattice (wherein one set of notes is connected with those containing it). If one excludes modes with 0, 1, 11 or 12 notes which can be construed as too extreme, there are 15 generalized Messiaen modes which are represented on clock diagrams. Some of the ones omitted by Messiaen are arguably of musical importance, like the hexatonic collection 0 1 4 5 8 9. The augmented scale: 0 3 4 7 8 11 (Root, minor 3rd, major 3rd, 5th, augmented 5th, major 7th, or minor 3rd, semitone, minor 3rd, semitone, minor 3rd, semitone) may appear to be an inexplicable omission on Messiaen's part. It is a symmetrical scale used frequently by modern jazz improvisers. However closer inspection reveals it to be a truncated version of his Third Mode.

All 15 MTL

Truncation

Truncation involves the removal of notes from one of the modes to leave a new truncated mode. Both the notes removed and the notes remaining must preserve the symmetry of the parent mode, and must therefore fulfill the conditions for limited transposition. For example, consider mode 1.

• C D E F♯ G♯ A♯

Removing alternate notes creates a new truncated mode of limited transposition.

• C E G♯

Removing two notes for every one kept creates a new truncated mode of limited transposition.

• C F♯

Keeping two notes for every one removed creates another truncated mode of limited transposition.

• C E F♯ A♯

Only Messiaen's mode 7 and mode 3 are not truncated modes: the other modes may be constructed from them or from one or more of their modes. Mode 7 contains modes 1, 2, 4, 5, and 6. Mode 6 contains modes 1 and 5. Mode 4 contains mode 5. Mode 3 contains mode 1.

Pure intervallic truncations

• Tritones, truncation of modes 1, 2, 3, 4, 5, 6 and 7: augmented fourth, augmented fourth – 1 mode and 6 transpositions
• Major thirds, truncation of modes 1, 3, 6 and 7: major third, major third, major third – 1 mode and 4 transpositions. See Augmented triad
• Minor thirds, truncation of modes 2, 4, 6 and 7: minor third, minor third, minor third, minor third – 1 mode and 3 transpositions. See Diminished seventh chord
• Whole tones (mode 1), truncation of modes 3, 6 and 7: tone, tone, tone, tone, tone, tone – 1 mode and 2 transpositions

Other truncations

• Truncation of modes 2, 4, 6 and 7: semitone, tone, minor third, semitone, tone, minor third – 3 modes, 6 transpositions. (Modes are "mirror" inversions of Petrushka Chord modes.)
• Truncation of modes 1, 2, 3, 4, 5, 6 and 7: major third, tone, major third, tone – 2 modes, 6 transpositions. See French Sixth and Dominant seventh flat five chord
• Truncation of modes 2, 3, 4, 5, 6 and 7: perfect fourth, semitone, perfect fourth, semitone – 2 modes, 6 transpositions. See 1:5 Distance model
• Truncation of mode 3: minor third, semitone, minor third, semitone, minor third, semitone – 2 modes, 4 transpositions. See augmented scale
• Truncation of modes 2, 4, 6 and 7: minor third, tone, semitone, minor third, tone, semitone – 3 modes, 6 transpositions. See Petrushka Chord

Use and sound

Messiaen found ways of employing all of the modes of limited transposition harmonically, melodically, and sometimes polyphonically. The whole-tone and octatonic scales have enjoyed quite widespread use since the turn of the 20th century, particularly by Debussy (the whole-tone scale) and Stravinsky (the octatonic scale).

The symmetry inherent in these modes (which means no note can be perceived as the tonic), together with certain rhythmic devices, Messiaen described as containing "the charm of impossibilities".

The composer Tōru Takemitsu made frequent use of Messiaen's modes, particularly the third mode. The composer Alexander Tcherepnin has adopted the third mode as one of his synthetic scales, and it is known as the "Tcherepnin scale".

In other temperaments

There are no modes of limited transposition in any prime equal division of the octave, such as 19 equal temperament or 31 equal temperament.

Composite divisions, such as 15 equal temperament or 22 equal temperament, have them. The 12-note chromatic scale can itself be considered such a mode when viewed as a subset of a larger system that contains it, such as quarter tones or 72 equal temperament.

8-tet
Scale step	0	1	2	3	4	5	6	7
Cents	0	150	300	450	600	750	900	1050
Note	C	D/C	E♭/D♯	F/E	G♭/F♯	A/G	A	B/A

For example, eight equal temperament, the lowest non-prime equal temperament not completely included in 12-tet (due to a scale step in 24-tet), would have modes of limited transposition. The first would be 0, 2, 4, 6 (steps: 2222), which has only two transpositions and one mode. Another would be 0, 1, 4, 5 (steps: 1313 and 3131), which has 4 transpositions and 2 modes (the other is 0, 3, 4, 7).

Further reading

• Anaf, Jef. 1988. "Olivier Messiaen 80 jaar: Nog steeds actief mit zijn modale toonstelsel". Adem: Driemaandelijks tijdschrift voor muziek cultuur 24, no. 4 (October–December): 184–91.
• Douthett, Jack, and Peter Steinbach. 1998. "Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition". Journal of Music Theory 42, no. 2 (Fall): 241–63.
• Frischknecht, Hans Eugen. 2008. "Potential und Grenzen einer musikalischen Sprache: Olivier Messiaens modes à transpositions limitées unter der Lupe". Dissonanz/Dissonance, no. 104 (December): 32–34.
• Giesl, Peter. 2002. "Zur melodischen Verwendung des Zweiten Modus in Messiaens Subtilité des Corps Glorieux". In Musik, Wissenschaft und ihre Vermittlung: Bericht über die internationale musikwissenschaftliche Tagung der Hochschule für Musik und Theater Hannover, edited by Arnfried Edler and Sabine Meine, 259–64. Publikationen der Hochschule für Musik und Theater Hannover 12. Augsburg: Wißner. ISBN 3-89639-342-1.
• Neidhöfer, Christoph. 2005. "A Theory of Harmony and Voice Leading for the Music of Olivier Messiaen". Music Theory Spectrum 27, no. 1 (Spring): 1–34.
• Schuster-Craig, John. 1990. "An Eighth Mode of Limited Transposition". The Music Review 51, no. 4 (November) : 296–306.
• Street, Donald. 1976. "The Modes of Limited Transposition". The Musical Times 117, no. 1604 (October): 819–23.
• Yamaguchi, Masaya. 2006. The Complete Thesaurus of Musical Scales, revised edition. New York: Masaya Music Services. ISBN 0-9676353-0-6.
• Yamaguchi, Masaya. 2006. Symmetrical Scales for Jazz Improvisation, revised edition. New York: Masaya Music Services. ISBN 0-9676353-2-2.
• Yamaguchi, Masaya. 2012. Lexicon of Geometric Patterns for Jazz Improvisation. New York: Masaya Music Services. ISBN 0-9676353-3-0.

External links

• My Messiaen Modes – A visual representation of the modes of limited transposition