Exeligmos

An exeligmos (Ancient Greek: ἐξελιγμός, lit. 'turning of the wheel') is a period of 54 years, 33 days that can be used to predict successive eclipses with similar properties and location. For a solar eclipse, after every exeligmos a solar eclipse of similar characteristics will occur in a location close to the eclipse before it. For a lunar eclipse the same part of the earth will view an eclipse that is very similar to the one that occurred one exeligmos before it (see main text for visual examples). The exeligmos is an eclipse cycle that is a triple saros, three saroses (or saroi) long, with the advantage that it has nearly an integer number of days so the next eclipse will be visible at locations and times near the eclipse that occurred one exeligmos earlier. In contrast, each saros, an eclipse occurs about eight hours later in the day or about 120° to the west of the eclipse that occurred one saros earlier.^[1]

It corresponds to:

3 saroses
669 synodic months
725.996 draconic months
56.996 eclipse years (114 eclipse seasons)
716.976 anomalistic months

The 57 eclipse years means that if there is a solar eclipse (or lunar eclipse), then after one exeligmos a New Moon (resp. Full Moon) will take place at the same node of the orbit of the Moon, and under these circumstances another eclipse can occur.

Details

The Greeks had knowledge of the exeligmos by at latest 100 BC. A Greek astronomical clock called the Antikythera mechanism used epicyclic gearing to predict the dates of consecutive exeligmoses.^[2]

The exeligmos is 669 synodic months (every eclipse cycle must be an integer number of synodic months), almost exactly 726 draconic months (which ensures the sun and moon are in alignment during the new moon), and also almost exactly 717 anomalistic months^[3] (ensuring the moon is at the same point of its elliptic orbit). It also corresponds to 114 eclipse seasons. The first two factors make this a long-lasting eclipse series. The latter factor is what makes all the eclipses in an exeligmos so similar. The near-integer number of anomalistic months ensures that the apparent diameter of the moon will be nearly the same with each successive eclipse. The fact that it is very nearly a whole integer of days ensures each successive eclipse in the series occurs very close to the previous eclipse in the series. For each successive eclipse in an exeligmos series the longitude and latitude can change significantly because an exeligmos is over a month longer than a calendar year, and the gamma increases/decreases because an exeligmos is about three hours shorter than a draconic month. The sun's apparent diameter also changes significantly in one month, affecting the length and width of a solar eclipse.^[1]

Solar exeligmos example

Here is a comparison of two annular solar eclipses one exeligmos apart:

	May 20, 1966	June 21, 2020
Path Map (annular eclipse is red path) (light blue lines are lines of obscuration of 0%, 20%, 40%, 60% and 80% covered)
Duration	0 minutes 5 seconds	0 minutes 38 seconds
Max width of annular eclipse path	3 kilometers	21 kilometers
Latitude of greatest eclipse	39° North	31° North
Time of greatest eclipse (UTC)	09:38	06:40

Lunar exeligmos example

Here is a comparison of two total lunar eclipses one exeligmos apart:

	December 30, 1963	January 31, 2018
Path Map
Visibility (side of earth eclipse is visible from)
Duration (Partial eclipse)	204 minutes	203 minutes
Time of greatest eclipse (UTC)	11:06	13:29

Sample series of solar exeligmos

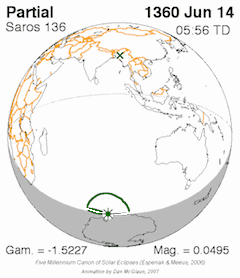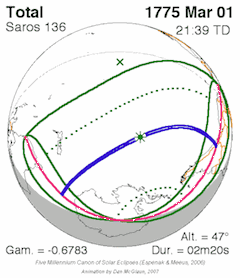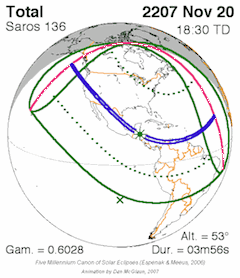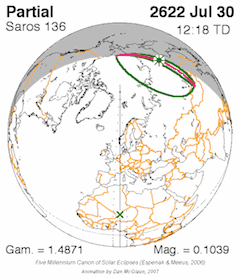
Exeligmos table of solar saros 136. Each eclipse occurs at roughly the same longitude but moves about 5-15 degrees in latitude with each successive cycle.^[1]

Saros	Member	Date^[4]	Time (Greatest) UTC	Type	Location Lat,Long	Gamma	Mag.	Width (km)	Duration (min:sec)	Ref
136	3	July 5, 1396	19:37:40	Partial	63.9S 147.2W	-1.3568	0.3449			[1]
136	6	August 7, 1450	16:48:49	Partial	61.8S 132.8W	-1.1286	0.756			[2]
136	9	September 8, 1504	15:12:15	Annular	55.3S 102.6W	-0.9486	0.9924	83	0m 32s	[3]
136	12	October 11, 1558	14:58:55	Annular	56.5S 90.3W	-0.8289	0.9971	18	0m 12s	[4]
136	15	November 22, 1612	16:04:35	Hybrid	65.7S 98.4W	-0.7691	1.0002	1	0m 1s	[5]
136	18	December 25, 1666	17:59:16	Hybrid	71.6S 98.3W	-0.7452	1.0058	30	0m 24s	[6]
136	21	January 27, 1721	20:05:11	Total	64S 102.4W	-0.7269	1.0158	79	1m 7s	[7]
136	24	March 1, 1775	21:39:20	Total	47.9S 124.8W	-0.6783	1.0304	139	2m 20s	[8]
136	27	April 3, 1829	22:18:36	Total	28.5S 142.6W	-0.5803	1.0474	192	4m 5s	[9]
136	30	May 6, 1883	21:53:49	Total	8.1S 144.6W	-0.425	1.0634	229	5m 58s	[10]
136	33	June 8, 1937	20:41:02	Total	9.9N 130.5W	-0.2253	1.0751	250	7m 4s	[11]
136	36	July 11, 1991	19:07:01	Total	22N 105.2W	-0.0041	1.08	258	6m 53s	[12]
136	39	August 12, 2045	17:42:39	Total	25.9N 78.5W	0.2116	1.0774	256	6m 6s	[13]
136	42	September 14, 2099	16:57:53	Total	23.4N 62.8W	0.3942	1.0684	241	5m 18s	[14]
136	45	October 17, 2153	17:12:18	Total	18.8N 65.7W	0.5259	1.056	214	4m 36s	[15]
136	48	November 20, 2207	18:30:26	Total	15.8N 87.8W	0.6027	1.0434	180	3m 56s	[16]
136	51	December 22, 2261	20:38:50	Total	16.1N 124.2W	0.636	1.0337	147	3m 17s	[17]
136	54	January 25, 2316	23:05:17	Total	21.4N 166W	0.6526	1.0282	126	2m 42s	[18]
136	57	February 27, 2370	1:07:02	Total	33.2N 157E	0.6865	1.0262	121	2m 17s	[19]
136	60	March 31, 2424	2:10:10	Total	51.3N 131.9E	0.7652	1.0254	133	1m 55s	[20]
136	63	May 3, 2478	1:55:59	Total	75.7N 107.7E	0.9034	1.0218	176	1m 20s	[21]
136	66	June 5, 2532	0:28:58	Partial	67.5N 1.3E	1.0962	0.8224			[22]
136	69	July 7, 2586	22:07:07	Partial	64.5N 7.2E	1.327	0.3957			[23]

Solar exeligmos animation

Here is an animation of an exeligmos series. Note the similar paths of each total eclipse, and how they fall close to the same longitude of the earth.^[5]

Solar Saros Animation (for comparison)

This next animation is from the entire saros series of the exeligmos above. Notice how each eclipse falls on a different side of the earth (120 degrees apart).^[5]

References

^ ^a ^b ^c Littman, Mark; et al. (2008). Totality: eclipses of the sun. Oxford University Press. pp. 325–326. ISBN 978-0-19-953209-4.
^ Freeth, Tony; Y. Bitsakis; X. Moussas; M.G. Edmunds (November 30, 2006). "Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism". Nature. 444 (7119): 587–591. Bibcode:2006Natur.444..587F. doi:10.1038/nature05357. PMID 17136087.
^ David, Furley (11 February 1999). From Aristotle to Augustine. Psychology Press. p. 301. ISBN 978-0-415-06002-8 – via Google Books.
^ Gregorian Calendar is used for dates after 1582 Oct 15. Julian Calendar is used for dates before 1582 Oct 04.
^ ^a ^b NASA Eclipse Website Fred Espenak

[Totality-1] Littman, Mark; et al. (2008). Totality: eclipses of the sun. Oxford University Press. pp. 325–326. ISBN 978-0-19-953209-4.

[2] Freeth, Tony; Y. Bitsakis; X. Moussas; M.G. Edmunds (November 30, 2006). "Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism". Nature. 444 (7119): 587–591. Bibcode:2006Natur.444..587F. doi:10.1038/nature05357. PMID 17136087.

[3] David, Furley (11 February 1999). From Aristotle to Augustine. Psychology Press. p. 301. ISBN 978-0-415-06002-8 – via Google Books.

[4] Gregorian Calendar is used for dates after 1582 Oct 15. Julian Calendar is used for dates before 1582 Oct 04.

[NASA-5] NASA Eclipse Website Fred Espenak

[1]

[2]

[3]

[4]

[5]