Hexahedron
A hexahedron (pl.: hexahedra or hexahedrons) or sexahedron (pl.: sexahedra or sexahedrons) is any polyhedron with six faces. A cube, for example, is a regular hexahedron with all its faces square, and three squares around each vertex.
There are seven topologically distinct convex hexahedra,[1] one of which exists in two mirror image forms. Additional non-convex hexahedra exist, with their number depending on how polyhedra are defined. Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.
Convex, Cuboid
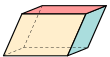
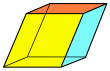
[edit]A hexahedron that is combinatorially equivalent to a cube may be called a cuboid, although this term is often used more specifically to mean a rectangular cuboid, a hexahedron with six rectangular sides. Different types of cuboids include the ones depicted and linked below.
| Cuboids | ||||||
|---|---|---|---|---|---|---|

|

|

|

|

|
|
|
| Cube (square) |
Rectangular cuboid (three pairs of rectangles) |
Trigonal trapezohedron (congruent rhombi) |
Trigonal trapezohedron (congruent quadrilaterals) |
Quadrilateral frustum (apex-truncated square pyramid) |
Parallelepiped (three pairs of parallelograms) |
Rhombohedron (three pairs of rhombi) |
Convex, others
[edit]There are seven topologically distinct convex hexahedra,[1] the cuboid and six others, which are depicted below. One of these is chiral, in the sense that it cannot be deformed into its mirror image.
| Image | 
|
 
|

|

|

|

|
|---|---|---|---|---|---|---|
| Name | Triangular bipyramid | Pentagonal pyramid | Doubly truncated tetrahedron[2] | |||
| Features |
|
|
|
|
|
|
| Properties | Simplicial | Dome |
Concave
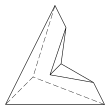
[edit]Three further topologically distinct hexahedra can only be realised as concave acoptic polyhedra. These are defined as the surfaces formed by non-crossing simple polygon faces, with each edge shared by exactly two faces and each vertex surrounded by a cycle of three or more faces.[3]
| Concave | ||
|---|---|---|

|

|
|
| 4.4.3.3.3.3 Faces 10 E, 6 V |
5.5.3.3.3.3 Faces 11 E, 7 V |
6.6.3.3.3.3 Faces 12 E, 8 V |
These cannot be convex because they do not meet the conditions of Steinitz's theorem, which states that convex polyhedra have vertices and edges that form 3-vertex-connected graphs.[4] For other types of polyhedra that allow faces that are not simple polygons, such as the spherical polyhedra of Hong and Nagamochi, more possibilities exist.[5]
References
[edit]- ^ a b Dillencourt, Michael B. (1996), "Polyhedra of small order and their Hamiltonian properties", Journal of Combinatorial Theory, Series B, 66 (1): 87–122, doi:10.1006/jctb.1996.0008, MR 1368518
- ^ Kolpakov, Alexander; Murakami, Jun (2013), "Volume of a doubly truncated hyperbolic tetrahedron", Aequationes Mathematicae, 85 (3): 449–463, doi:10.1007/s00010-012-0153-y, MR 3063880
- ^ Grünbaum, Branko (1999), "Acoptic polyhedra" (PDF), Advances in discrete and computational geometry (South Hadley, MA, 1996), Contemporary Mathematics, vol. 223, Providence, Rhode Island: American Mathematical Society, pp. 163–199, doi:10.1090/conm/223/03137, ISBN 978-0-8218-0674-6, MR 1661382; for the three non-convex acoptic hexahedra see p. 7 of the preprint version and Fig. 3, p. 30
- ^ Ziegler, Günter M. (1995), "Chapter 4: Steinitz' Theorem for 3-Polytopes", Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Springer-Verlag, pp. 103–126, ISBN 0-387-94365-X
- ^ Hong, Seok-Hee; Nagamochi, Hiroshi (2011), "Extending Steinitz's theorem to upward star-shaped polyhedra and spherical polyhedra", Algorithmica, 61 (4): 1022–1076, doi:10.1007/s00453-011-9570-x, MR 2852056
